排序算法
约 3043 字大约 10 分钟
2025-02-12
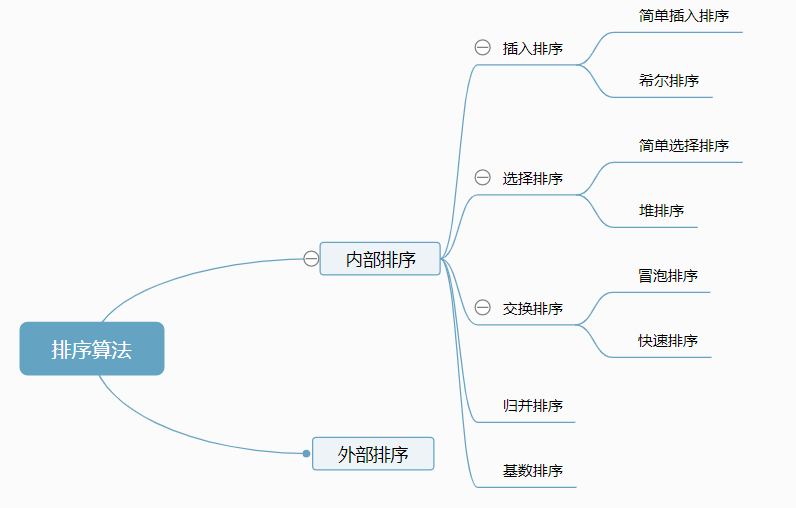
1 简单插入排序
算法逻辑也很简单,从index=1开始,与前面的数比较大小比前面的数字大或者相等,则不动比前面的数字小,则前面的数字依次往后移动一位,直到比前面的数字大或者相等,插入空闲的位置
(稳定)
public static void insertSort(int[] arr) {
// 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for (int i=1;i<arr.length;i++) {
// 记录要插入的数据
int temp = arr[i];
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
while (j>0 && temp<arr[j-1]) {
arr[j] = arr[j-1];
j--;
}
// 存在比其小的数,插入
if (j!=i) {
arr[j] = temp;
}
}
}2 希尔排序
选择增量 gap=length/2,缩小增量继续以gap = gap/2(例如length=10,gap分别是5,2,1)gap=5时,数组里下标为0,5进行插入排序,1,6进行插入排序…gap=2时,数组里下标为0,2,4,6,8进行插入排序,1,3,5,7,9进行插入排序gap=1时,数组里下标为0,1,2,3,4,5,6,7,8,9进行插入排序
(不稳定)
public static void shellSort(int[] arr) {
// gap慢慢减小 - 5,2,1
for (int gap=arr.length/2; gap>0; gap/=2) {
// gap=5时,i=5,6,7,8,9
// gap=2时,i=2,3,4,5,6,7,8,9
for (int i=gap;i<arr.length; i++) {
int temp = arr[i];// 记录需要判断的数字
int j = i - gap;// 记录判断数字的前一个位置
// 进入while则代表判断数字小于前面某数字
while (j>=0 && temp<arr[j]) {
arr[j+gap] = arr[j];// 前面数字往后移动
j -= gap;
}
arr[j+gap] = temp;// 放入最后的空闲位置
}
}
}3 简单选择排序
寻找到数组里最小的数字,和起始位置数字交换继续寻找数字里剩下的最小数字,和未排序的起始位置数字交换
(不稳定)
public static void SelectionSort(int[] arr) {
// 总共要经过 N-1 轮比较
for (int i=0;i<arr.length-1;i++) {
int min = i;// 最开始假定选中的数字就是最小的
// 每轮需要比较的次数 N-i
for (int j=i+1;j<arr.length;j++) {
if (arr[j]<arr[min]) {
// 记录目前能找到的最小值元素的下标
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
if (i!=min) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
}4 堆排序
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
大顶堆的构建方法:从最后一个非叶子结点开始( arr.length/2-1),从左至右,从下至上进行调整判断与子节点的大小,如果子节点更大则交换 (小顶堆则相反)
堆排序构建方法:先将原始数组构建成大顶堆(升序)或小顶堆(降序)再将堆顶元素与末尾元素交换,满足最大(小)值到数组最后以根节点为开始,重新构建堆
4.1 递归写法
public static void HeapSort(int[] arr) {
int len = arr.length;
// 构建初始大顶堆
buildMaxHeap(arr, len);
for (int i=len-1;i>0;i--) {
// 堆顶元素与末尾元素(除了已经交换到末尾的,所以这里写入i,而不是len-1)交换
swap(arr, 0, i);
// 排好序的数组位置(从末尾开始)就不用再使用大顶堆排序了
len--;
// 根节点开始,重新构建堆
heapify(arr, 0, len);
}
}
private static void buildMaxHeap(int[] arr, int len) {
for (int i=len/2-1;i>=0;i--) {
heapify(arr, i, len);
}
}
private static void heapify(int[] arr, int i, int len) {
int left = 2*i+1;
int right = 2*i+2;
int largest = i;
if (left<len && arr[left] > arr[largest]) {
largest = left;
}
if (right<len && arr[right] > arr[largest]) {
largest = right;
}
// 说明子节点大于父节点,交换,然后把子节点当作父节点,进行堆排序
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest, len);
}
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}4.2 非递归写法
public static void HeapSort(int[] arr) {
int len = arr.length;
// 构建初始大顶堆
buildMaxHeap(arr, len);
// 调整堆结构+交换堆顶元素与末尾元素
for (int i=len-1;i>0;i--) {
// 堆顶元素与末尾元素(除了已经交换到末尾的,所以这里写入i,而不是len-1)交换
swap(arr, 0, i);
// 排好序的数组位置(从末尾开始)就不用再使用大顶堆排序了
len--;
// 根节点开始,重新构建堆
heapify(arr, 0, len);
}
}
private static void buildMaxHeap(int[] arr, int len) {
for (int i=len/2-1;i>=0;i--) {
heapify(arr, i, len);
}
}
private static void heapify(int []arr,int i,int length){
int temp = arr[i];//先取出当前元素i
// 从左子结点开始
for (int k=i*2+1;k<length;k=k*2+1) {
// 如果左子结点小于右子结点
if (k+1<length && arr[k]<arr[k+1]) {
k++;
}
//如果子节点大于父节点,将子节点值赋给父节点
if (arr[k] > temp) {
arr[i] = arr[k];
i = k;
} else {
break;
}
}
//将temp值放到最终的位置
arr[i] = temp;
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}5 冒泡排序
冒泡排序也简单,从头到尾相邻两个数比较,前面的数比后面的数大则交换,可以达到最后一个数是最大的数组里再去掉最后一个数,对前面的数进行相同的逻辑
public static void sort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
// 设定一个标记,若为true,则表示此次循环没有进行交换,也就是待排序列已经有序,排序已经完成。
boolean flag = true;
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = false;
}
}
if (flag) {
break;
}
}
}6 快速排序
《算法艺术与信息学竞赛》——快速排序的最坏运行情况是 O(n²),比如说顺序数列的快排。
但它的平摊期望时间是 O(nlogn),且 O(nlogn) 记号中隐含的常数因子很小,比复杂度稳定等于 O(nlogn) 的归并排序要小很多。
所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。
问题1:为什么 if(start >= end) return;中是>=?
答:首先>肯定是必备的,毋庸置疑。写等于是因为,当start和end相等的时候不就指向一个数吗,无需在将这个一个数的子数组快排
问题2:为什么是while(array[j]>=key && i < j) 和 while(array[i]<=key && i < j)?
答:先说array[j]>=key和array[i]<=key中为什么要有等于,因为避免进入死循环。如果数组是一个全是相等的数(比如全是1)的数组,那么不加等于的话,i和j不会加减,**循环不会跳出。**好,那现在加上等于了,还是哪个例子,**下标越界了。**因为ij0的时候,j继续减1,自然下标越界。所以要加上 && i < j
6.1 左右指针法
数组中挑一个数作为基准(第一个或最后一个),10,7,2,4,7,62,3,4,2,1,8,9,19(以第一个举例)10是基准以最左边和最右边两个数作为指针left和right,10是left,19是right
left指针从左至右找到比基准大的数,right指针从右至左找到比基准小的数,然后交换left和right最终会相遇,基准再和right(left)交换最后再对基准左右的子数组分别进行左右指针法
public static void sort(int []array, int start, int end) {
if(start >= end)
return;
int i = start;
int j = end;
int key = array[start];
while(i < j) {
while(array[j]>=key && i < j)
j--;
while(array[i]<=key && i < j)
i++;
swap(array, i, j);
}
swap(array, start, j);
sort(array, start, j-1);
sort(array, j+1, end);
}
public static void swap(int []array,int i,int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}6.2 填坑法
刚开始的基准位即第一个坑位
数组中挑一个数作为基准(第一个或最后一个),10,7,2,4,7,62,3,4,2,1,8,9,19(以第一个举例)10是基准以最左边和最右边两个数作为指针left和right,10是left,19是right
取第一个数作为基准时,right指针(先)从右至左找到比基准小的数,然后再走left取最后一个数作为基准时,left指针(先)从左至右找到比基准大的数,然后再走right找到数的时候就放到坑位里(为什么取第一个数先走right呢,因为这是从小到大排,后面大的数要交换到前面)
left和right最终会相遇,再对刚开始基准的数(第一个坑位的数)放到right(left)的位置上最后再对基准左右的子数组分别进行填坑法
public static void sort(int []array, int start, int end) {
if(start >= end)
return;
int i = start;
int j = end;
int key = array[start];
while(i < j) {
while(array[j]>=key && i < j)
j--;
array[i] = array[j];
while(array[i]<=key && i < j)
i++;
array[j] = array[i];
}
array[j] = key;
sort(array, start, j-1);
sort(array, j+1, end);
}还有一种前后指针法,和非递归(用栈实现)的快排方法。
- 前后指针法的优势在于可以对链表排序。
- 非递归的快排用栈实现。——递归的算法主要是在划分子区间,如果要非递归实现快排,只要使用一个栈来保存区间就可以了。 一般将递归程序改成非递归首先想到的就是使用栈,因为递归本身就是一个压栈的过程
7 归并排序
10,7,2,4,3,1,8,9 - 以这8个数为例,分成两组{10,7,2,4} {3,1,8,9} - 每个组再分成两组{[10,7] [2,4]} {[3,1] [8,9]} - 每个组再分成两组{[(10)(7)] [(2)(4)]} {[(3)(1)] [(8)(9)]} - 已经分到最小
创建temp数组,存放比较后的数字例如 [7,10] [2,4]比较后temp放入顺序是 2 4 7 10,(比较过程是7与2比2放入,7与4比4放入,7 10直接放入)最后会是{2,4,7,10} {1,3,8,9}比较(比较过程是2与1比1放入,2与3比2放入,4与3比3放入这样….)
// 菜鸟教程版本,用Arrays参数
public int[] sort(int[] arr) {
if (arr.length < 2) {
return arr;
}
int middle = (int) Math.floor(arr.length / 2);
int[] left = Arrays.copyOfRange(arr, 0, middle);
int[] right = Arrays.copyOfRange(arr, middle, arr.length);
return merge(sort(left), sort(right));
}
protected int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0;
while (left.length > 0 && right.length > 0) {
if (left[0] <= right[0]) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
} else {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
}
while (left.length > 0) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
}
while (right.length > 0) {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
return result;
}
// [网上大神版本](https://www.cnblogs.com/chengxiao/p/6194356.html)
public static void sort(int []arr){
//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
int []temp = new int[arr.length];
sort(arr,0,arr.length-1,temp);
}
private static void sort(int[] arr,int left,int right,int []temp){
if(left<right){
int mid = (left+right)/2;
sort(arr,left,mid,temp);//左边归并排序,使得左子序列有序
sort(arr,mid+1,right,temp);//右边归并排序,使得右子序列有序
merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
}
}
private static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i = left;//左序列指针
int j = mid+1;//右序列指针
int t = 0;//临时数组指针
while (i<=mid && j<=right){
if(arr[i]<=arr[j]){
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
while(i<=mid){//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while(j<=right){//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while(left <= right){
arr[left++] = temp[t++];
}
}8 基数排序
呃,暂略… -,-
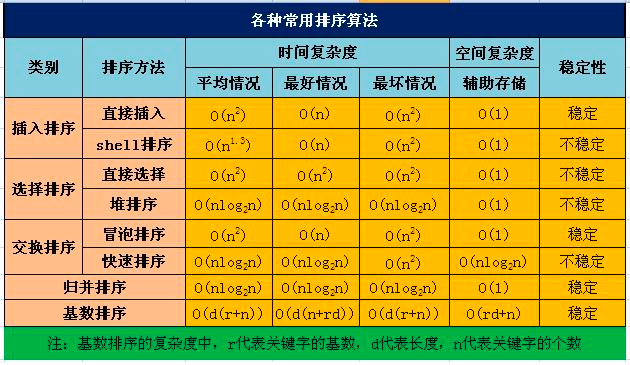
9 总结